|
|
|
|
|
|
|
[38]
D.Kinzebulatov,
Yu.A. Semenov
"Feller
generators
with drifts in
the critical
range", Preprint, arXiv:2405.12332 2405.12332.pdf
We
construct
strongly
continuous
Feller
semigroup
associated to
Kolmogorov-Fokker-Planck
operator
covering for
the first time
the entire
range of
strengths of
critical
singularities
of the drift.
Our main
instrument is
De Giorgi's
method in Lp.
[37]
D.Kinzebulatov
"Non-local
parabolic
equations with
singular
(Morrey)
time-inhomogeneous
drift",
Preprint,
arXiv:2405.08652 2405.08652.pdf
We
obtain Sobolev
regularity
estimates for
solutions of
non-local
parabolic
equations with
locally
unbounded
drift
satisfying
some minimal
assumptions.
These results
yield Krylov
bound for the
corresponding
Feller stable
process as
well as some a
priori
regularity
estimates on
solutions of
McKean-Vlasov
equations. A
key element of
our arguments
is a parabolic
operator norm
inequality
that we prove
using some
ideas of Adams
and Krylov.
[36]
D.Kinzebulatov
"On
particle
systems and
critical
strengths of
general
singular
interactions", Preprint,
arXiv:2402.17009
2402.17009.pdf
For
finite
interacting
particle
systems with
strong
repulsing-attracting
or general
interactions,
we prove
global weak
well-posedness
almost up to
the critical
threshold of
the strengths
of attracting
interactions
(independent
of the number
of particles),
and establish
other
regularity
results, such
as a heat
kernel bound
in the regions
where strongly
attracting
particles are
close to each
other. Our
main analytic
instruments
are a variant
of De Giorgi's
method in L^p
and an
abstract
desingularization
theorem.
[35]
D.Kinzebulatov
"Laplacian
with singular
drift in a
critical
borderline
case", Preprint, arXiv:2309.04436 2309.04436.pdf
We
reach the
critical
magnitude of
form-bounded
drifts. The
corresponding
strong
well-posedness
theory of the
parabolic
diffusion
equation is
developed in
an Orlicz
space that is,
basically,
dictated by
the drift
term.
[34]
D.Kinzebulatov,
K.R. Madou "Strong
solutions of
SDEs with
singular
(form-bounded)
drift via
Roeckner-Zhao
approach",
Preprint,
arXiv:2306.04825
2306.04825.pdf
We
use the
approach of
Roeckner-Zhao
to prove
strong
well-posedness
for SDEs with
singular drift
satisfying
some minimal
assumptions.
[33]
SURVEY
D.Kinzebulatov
"Form-boundedness
and SDEs with
singular
drift", INdAM Meeting 2022: Kolmogorov Operators and Their
Applications,
2305.00146.pdf
We
survey and
refine recent
results on
weak
well-posedness
of SDEs with
singular drift
satisfying
some minimal
assumptions.
[32]
D.Kinzebulatov,
Yu.A.Semenov "Remarks
on parabolic
Kolmogorov
operator",
Preprint,
arXiv:2303.03993
2303.03993.pdf
We
establish
gradient
estimates
needed to
study
parabolic
equations and
SDEs with
time-inhomogeneous
singular
drifts.
[31]
D.Kinzebulatov
"Parabolic
equations and
SDEs with
time-inhomogeneous
Morrey drift",
Preprint,
arXiv:2301.13805
2301.13805.pdf
We
prove
existence and
uniqueness of
weak solution
of SDE with
singular drift
in a very
large class
(essentially,
the largest
scaling-invariant
Morrey class).
[30]
D.Kinzebulatov,
R.Vafadar "On
divergence-free
(form-bounded
type)
drifts", Discrete Contin. Dyn.
Syst. Ser. S,
17 (2024),
2083-2107,
2209.04537.pdf
We
prove a
posteriori
Harnack
inequality for
elliptic
equation with
divergence-free
singular
drift. A key
step in our
proofs is a
new iteration
procedure used
in addition to
the classical
De Giorgi's
iterations and
Moser's
method.
[29]
D.Kinzebulatov,
Yu.A.Semenov "Regularity
for parabolic
equations with
singular
non-zero
divergence
vector fields",
J.
Differential
Equations,
to
appear 2205.05169.pdf
We prove
Gaussian
bounds on the
heat kernel of
parabolic
equation with
singular drift
having
singular
divergence,
taking into
account
possible
cancellation
phenomena.
[28]
R. Gibara,
D.Kinzebulatov
"On the
vanishing of
Green's
function,
desingularization
and Carleman's
method",
St. Petersburg Math. J. (Algebra i
Analiz), 35(3)
(2023) 2202.10528.pdf
We
establish
quantiative
estimates on
the order of
vanishing of
Green's
function of
Schroedinger
operator under
minimal
assumptions on
the potential
(i.e.
form-boundedness,
which ensures
that the
Schroedinger
operator is
well defined
in L2). The
proofs use
Carleman's
method.
[27]
D.
Kinzebulatov,
Yu.A. Semenov
"Sharp
solvability for
singular SDEs",
Electron. J. Probab., 28 (2023), article no.
69, 1–15. 2110.11232.pdf
The attracting Hardy drift provides a counterexample to
weak
solvability of
SDEs if the
coefficient of
the drift is
larger than a
certain
critical
threshold. We
prove a
positive
well-posednss
result,
reaching this
critical
threshold from
below, for the
entire class
of
form-bounded
drifts.
[26]
D.
Kinzebulatov,
K.R. Madou,
Yu.A. Semenov
"On the
supercritical
fractional
diffusion
equation with
Hardy-type
drift",
J.
d'Analyse
Mathématique,
to appear 2112.06329.pdf (2021)
We
consider
fractional
diffusion
operator with
a drift in the
supercritical
case, i.e.
when the drift
dominates the
diffusion. We
show that the
heat kernel
can vanish
even if the
drift is
Holder
continuous.
[25]
D.
Kinzebulatov,
K.R. Madou "Stochastic
equations with
time-dependent
singular drift",
J. Differential Equations, 337 (2022),
255-293 2105.07312.pdf
We
prove
existence and
uniqueness of
weak solution
to SDEs under
minimal
assumptions on
singular drift
(form-boundedness).
[24]
D.
Kinzebulatov,
Yu.A.
Semenov "Heat
kernel bounds
for parabolic
equations with
singular
(form-bounded)
vector fields",
Math. Ann., 384 (2022), 1883-1929 2103.11482.pdf
We
shed light on
the effect of
the positive
and negative parts of singular divergence of the drift on
the Gaussian
heat kernel
bounds. In
particular, we
establish for
the first time
and for a
large class of
drifts a
Gaussian lower
bound in the
situation
where there is
no Gaussian
upper bound.
[23] D.
Kinzebulatov,
Yu.A. Semenov
and R. Song "Stochastic
transport
equation with
singular drift",
Ann. Inst. Henri Poincaré (B) Probab. Stat., to
appear 2102.10610.pdf
We
establish
well-posedness
of stochastic
transport and
continuity
equations with
singular drift
in a large
class, which
allows to
address the
problem of
strong
well-posedness
of the
corresponding
SDEs.
[22] D.
Kinzebulatov,
Yu.A.
Semenov "Kolmogorov
operator with
the vector
field in Nash
class",
Tohoku Math. J., 74(4) (2022), 569-596 2012.02843.pdf
We
develop
solution
theory, and
establish a
posteriori
Gaussian heat
kernel bounds,
for
divergence-form
parabolic
equation under
minimal
assumptions on
the drift,
such that
there is no
weak solution
theory in L2,
but there is
nevertheless a
strong
solution
theory in L1.
The proofs use
Nash's method.
[21] D.
Kinzebulatov,
Yu.A. Semenov
"Fractional
Kolmogorov
operator
and
desingularizing
weights",
Publ. Res. Inst. Math., Kyoto, to appear 2005.11199.pdf
This is a continuation of [19]. We establish sharp upper
and lower
bounds on the
heat kernel of
the fractional
Laplace
operator
perturbed by
repulsing
Hardy-type
drift by
transferring
it to
appropriate
weighted space
with singular
weight.
[20]
D.
Kinzebulatov,
K.R.
Madou "On
admissible
singular
drifts of
symmetric
alpha-stable
process",
Math.
Nachr.,
295(10)
(2022),
2036-2064 2002.07001.pdf
We
prove weak
well-posedness
of SDE driven
by stable
process under
minimal
assumptions on
singular drift.
[19] D.
Kinzebulatov Yu.A.
Semenov and K.
Szczypkowski "Heat
kernel of
fractional
Laplacian with
Hardy
drift
via desingularizing
weights",
J.
London Math.
Soc.,
104 (2021), p.
1861-1900 1904.07363.pdf
We
establish
sharp
two-sided
bounds on the
heat kernel of
the fractional
Laplacian,
perturbed by
the attracting
Hardy-type
drift having
critical-order
singularity,
using the
method of
desingularizing
weights. The
proofs use
some ideas of
J.Nash.
[18]
D.
Kinzebulatov,
Yu.A.
Semenov "Feller
generators and
stochastic
differential
equations with
singular
(form-bounded)
drift", Osaka J. Math., 58
(2021),
855–883 feller_sdes.pdf
Preprints 1803.06033.pdf
1904.01268.pdf
We
establish
weak-posedness
of Ito and
Stratonovich
SDEs under
minimal
assumptions on
singular drift
and
discontinuous
diffusion
coefficients.
[17] D.
Kinzebulatov
"Regularity theory of
Kolmogorov operator revisited", Canadian Bull.
Math. 64 (2021), p. 725-736 afb.pdf
Preprint 1807.07597.pdf
We develop a new approach to
regularity theory of diffusion operator with
singular drift, which allows to establish weak
well-posedness of the corresponding SDE.
[16]
D.
Kinzebulatov,
Yu.A. Semenov "Regularity of solutions to Kolmogorov
equation with Gilbarg-Serrin matrix", J. Evol. Equations, 22 (#
21) (2022) 1802.05167.pdf
We consider
divergence-form elliptic equations having critical
discontinuity in the matrix, and establish a
quantiative dependence between this discontinuity and
the regularity theory of these equations.
[15]
D.
Kinzebulatov,
Yu.A. Semenov
"Brownian
motion with
general drift",
Stoch.
Proc. Appl.
130 (2020), p.
2737-2750
(arXiv:1710.06729
1710.06729.pdf)
This
is the first
paper on weak
well-posedness
of SDE with
singular drift
that went
beyond the
popular Ld
class of
drifts.
|
|
|
[14] D.
Kinzebulatov,
Yu.A. Semenov "On the theory of the Kolmogorov
operator in the spaces $L^p$ and $C_\infty$", Ann. Sc. Norm. Super. Pisa
Cl. Sci. (5), 21 (2020), 1573-1647
(arXiv: 1709.08598.pdf)
This is a detailed
regularity theory of divergence-form elliptic
and parabolic operators with singular vector
field and discontinuous diffusion matrix.
|
|
|
[13] D.
Kinzebulatov "Feller
generators with measure-valued drifts", Potential Anal.,
48 (2018), p. 207-222 measure_perturb.pdf
We construct Feller process under
very broad assumptions on singular measure-valued drift,
using an interpla between two resolvent representations
(one not allowing measure-valued drifts, but providing
strong Sobolev regularity theory, and the other one
providing minimal theory but allowing to handle
measure-valued drifts).
|
|
|
|
|
|
[12]
D.
Kinzebulatov "A new approach to the
L^p-theory of -\Delta + b\grad,
and its applications to Feller
processes with general drifts", Ann. Sc. Norm. Super.
Pisa Cl. Sci. (5), 17
(2017), p. 685-711 diff_singular.pdf
Tl;dr: This is a major
advancement in the regularity theory of
diffusion operator with singular drift,
which allowed to go beyond the standard
classes of singular drifts (such as Kato
class or form-bounded drifts).
|
|
|
[11] D.
Kinzebulatov "Feller evolution families and
parabolic equations with form-bounded vector fields", Osaka J. Math., 54 (2017),
p. 499-516 feller.pdf
We construct
Feller evolution family for parabolic equation with
singular drift in a large class. The key element of
the proof is new gradient bounds and the parabolic
variant of the iteration procedure of
Kovalenko-Semenov.
[10] I. Binder, D.
Kinzebulatov
and M.Voda "Non-perturbative localization with
quasiperiodic potential in continuous time",
Comm. Math.
Phys., 351 (2017),
p. 1149-1175 s00220-016-2723-7.pdf
We establish Anderson localization
in continuous one-dimensional multifrequency
Schrödinger operators. This is a cointinuous analogue
of the result of Bourgain-Goldstein.
|
|
|
[9] A.Brudnyi, D.
Kinzebulatov
"Kohn decomposition for forms on coverings of complex
manifolds constrained along the fibres", Trans. Amer. Math. Soc.,
369 (2017), p. 167-186 kohn.pdf
We extend J.J. Kohn's Hodge-type
decomposition to the (p,q) Dolbeault cohomology groups
of spaces of differential forms taking values in certain
(possibly infinite-dimensional) holomorphic Banach
vector bundles.
|
|
|
[8] A.Brudnyi, D.
Kinzebulatov
"Towards
Oka-Cartan theory for algebras of holomorphic
functions on coverings of Stein manifolds I",
Revista Mat.
Iberoamericana, 31(4)
(2015), p. 1167-1230 bru_kinz_1.pdf
[7] A.Brudnyi, D.
Kinzebulatov
"Towards Oka-Cartan
theory for algebras of holomorphic functions on coverings of
Stein manifolds II", Revista Mat. Iberoamericana,
31(4) (2015), p.
989-1032 bru_kinz_2.pdf
We develop complex function theory for
some algebras of holomorphic functions on coverings of
Stein manifolds, including holomorphic almost periodic
functions.
|
|
|
[6] A.Brudnyi,
D.
Kinzebulatov
"Holomorphic almost periodic functions on coverings of
complex manifolds", New
York J. Math, 17a (2011), p. 267-300
nyjm.pdf
We establish some basic results of
complex analytic geometry on the maximal ideal spaces
of some algebras of holomorphic functions.
[5] D.
Kinzebulatov,
L. Shartser "Unique continuation for
Schroedinger
operators.
Towards an
optimal
result", J.Funct. Anal.,
258 (2010), p.
2662-2681 UC_jfa.pdf
This is the
strongest to date result on unique continuation
for eigenfunctions of Schroedinger operators, strengthening the
classical results of Stein, Jerison-Koenig,
Chanillo-Sawyer.
|
|
|
[4] A.Brudnyi, D.
Kinzebulatov
"Holomorphic
semi-almost periodic functions",
Integr.
Equ. Operat. Theory, 66
(2010), p.293-325 0911.0954v1.pdf
[3] A.Brudnyi, D.
Kinzebulatov
"On algebras of
holomorphic functons with semi-almost periodic
boundary values", C.
R. Math. Rep. Acad. Sci. Canada, 32
(2010), p.1-12
[2] A.Brudnyi, D.
Kinzebulatov "On uniform
subalgebras of L^\infty on the unit circle
generated by almost periodic functions", St. Petersburg Math. J.,
19 (2008), p.495-518 BK
- SPbJMath.pdf
Tl;dr: How does fixing
the type of discontinuity of boundary values of a
bounded holomorphic function F on the unit disk D
affects the properties of F inside of D? Lindelof
theorem states that the boundary values f=F|_{\partial
D} of F can not have first-kind discontinuities.
However, there are functions \Phi such that
\Phi(F)|_{\partial D} can be first-kind disconinuous. It
turns out that in the case \Phi(z)=|z| there is a
connection between bounded holomorphic functions on D
whose moduli can have only first-kind boundary
discontinuities and Sarason's semi-almost periodic
functions on \partial D (a priori, there is nothing
almost periodic about bounded holomorphic functions and
first-kind discontinuities!).
This link allows us to apply, in our
study, the results on almost periodic functions. In
particular, we establish for this algebra of bounded of
holomorphic functions:
- Grothendieck's approximation property (still a
conjecture for H^\infty(D)).
- Corona theorem.
- Results on completion of matrices with entries
in this algebra,
etc.
Our methods admit extension to subalgebras determined
by other functions \Phi.
|
|
|
[1] D.
Kinzebulatov "A
note of
Gagliardo-Nirenberg
type
inequalitities
on analytic
sets", C. R. Math. Rep.
Acad. Sci. Canada, 30 (2009), p.97-105. kinzebulatovC351.pdf
We
study a new local invariant of singularities of complex
analytic sets. This invariant arises as the 'correcting exponent' in
a family of Sobolev-type inequalities relating norms
of functions on these sets.
|
|
|
Algorithmic trading (2012-2014):
- A. Cartea,
S. Jaimungal and D.
Kinzebulatov
"Algorithmic trading with
learning", Int. J. Applied and Theoretical
Finance, 19, no.4, 1650028 (2016) (
http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2373196)
We propose a model where an
algorithmic trader takes a view on the distribution of
prices at a future date and then
decides how to trade in the direction of her
predictions using the optimal mix of market and limit orders.
Namely, we model the asset midquote price as a randomized Brownian
bridge S_t=S_0+\sigma\beta_{tT}+
tD/T
where D is a random
variable that encodes the trader's prior belief on the
asset's future price distribution, the noise term
\beta_{tT} is a standard Brownian bridge over time
interval independent of D. As time flows, the trader
learns the realized value of D.
- S.Jaimungal, D.
Kinzebulatov and
D.Rubisov
"Optimal accelerated share
repurchase", Applied. Math. Finance,
24, no.3 (2017) (http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2360394)
An accelerated share repurchase
(ASR) allows a fiirm to repurchase a significant portion
of its shares immediately, while shifting the burden of
reducing the impact and uncertainty in the trade to an
intermediary. The intermediary must then purchase the
shares from the market over several days, weeks, or as
much as several months. In this
work, we address the intermediary's optimal execution
and exit strategy taking into account the impact that
trading has on the market. We demonstrate that it is
optimal to exercise when the TWAP exceeds �\zeta(t)S_t,
where S_t is the fundamental price of the asset and
\zeta�(t) is deterministic. Moreover, we develop a
dimensional reduction of the Stochastic Control and
Stopping problem and implement an e�fficient numerical
scheme to compute the optimal trading and exit
strategies.
- S. Jaimungal, D.
Kinzebulatov
"Optimal execution with a price limiter", RISK, July 2014, http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2199889
|
|
|
|
|
|
Earlier
research while studying for B.Sc and M.Sc:
|
|
|
- D.
Kinzebulatov
"Systems
with distributions and viability theorem",
J. Math. Anal. Appl., 331 (2007), p. 1046-1067 kinz_viab.pdf
- V.Derr, D.
Kinzebulatov
"Dynamical
generalized functions and the multiplication
problem", Russian Math., 51 (2007), p.32-43 0603351.pdf
We study some ordinary
differential equations arising in singular optimal
control problems.
- E. Braverman, D.
Kinzebulatov
"Nicholson
blowfiles equation with a distributed delay", Canadian
Appl. Math. Q., 14 (2006), p.
107-128 brav_kinz.pdf
|
|
|
|
|
|
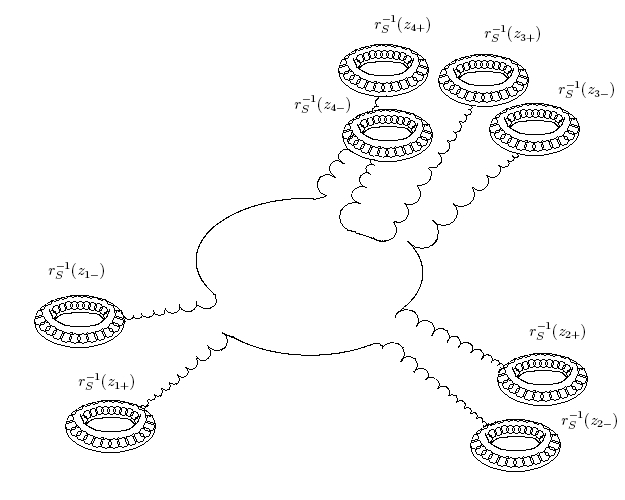
The topological structure of
the maximal ideal space of the algebra of
"semi-almost periodic" holomorphic functions in some
papers with A. Brudnyi
|
|


